Fisman et al.’s Psi (Ψ) index is ill-defined and leads to absurd interpretations

The unvaccinated cannot disproportionately infect the vaccinated (that was nonsense)

By Joseph Hickey and Denis G Rancourt

This report shows that modeling claims, based on a novel mathematical construction (Ψ), that unvaccinated people disproportionately contribute to the infection risk of vaccinated people are rigorously incorrect. It provides a mathematical proof that garbage science was published in the Canadian Medical Association Journal.

The report is published both by CORRELATION, and here: https://pubpeer.com/publications/3ACB55309DB4EF7D3518A4A5B2B65E#2 

The incorrect claims were made in the April 2022 article “Impact of population mixing between vaccinated and unvaccinated subpopulations on infectious disease dynamics: implications for SARS-CoV-2 transmission” by Fisman et al.

Hickey and Rancourt’s previous criticisms of the Fisman et al. article were:

• 2023-10-31: J. Hickey & D.G. Rancourt, “Viral respiratory epidemic modelling of societal segregation based on vaccination status”, medRxiv preprint [See Appendix 3 of Version 1 of the preprint, in particular]

• 2022-04-30: Interview about Fisman et al. paper with Dr. Byram Bridle and Dr. Denis Rancourt, Trish Wood is Critical Podcast

• 2022-04-29: D.G. Rancourt & J. Hickey, “Fisman et al.’s main conclusion does not follow from their model”, e-Letter, CMAJ

• 2022-04-27: D.G. Rancourt & J. Hickey, “OCLA Statement on CMAJ Fisman et al. Article Claiming Disproportionate Infection Risk from Unvaccinated Population, and on Negligent Media Reporting”

Here is the new report:

Fisman et al.’s Psi (Ψ) index is ill-defined and leads to absurd interpretations

By Hickey and Rancourt

Fisman et al. (2022) modeled an epidemic in a society with two interacting groups: vaccinated people and unvaccinated people.

Within their model setting, the authors sought to quantify “the contribution of risk to vaccinated people caused by infection acquired from contact with unvaccinated people” (Fisman et al., 2022, at pg. E575).

To achieve this objective, the authors should have used the fraction (B_v) of all infections among vaccinated people that derived from contact with unvaccinated people.

B_v is directly the risk of an infected vaccinated person having acquired their infection from an unvaccinated person. The said risk can then be evaluated as a function of the segregation of the two groups (η), vaccine efficacy (VE) or population fraction of vaccinated (P_v). In each case B_v has an immediate interpretation of interest to policy makers. This is done, for example, by Hickey and Rancourt (2022).

Furthermore, B_v is an outcome that directly can be used in calculations of other policy-relevant outcomes. For example, the fraction of the total population that is vaccinated and that became infected from unvaccinated persons, F_iu, is F_iu = P_vT_vB_v, where T_v is the fraction of the vaccinated population that became infected (the fraction of breakthrough infections on completion of the epidemic).

Instead of using B_v, the authors defined an index Ψ as “the fraction of all infections among vaccinated people that derived from contact with unvaccinated people [B_v], divided by the fraction of all contacts [involving vaccinated people] that occurred with unvaccinated people [f_vu]”.

Fisman et al. incorrectly interpreted their Ψ index, for example, as (Fisman et al., 2022, at pg. E575):

“As like-with-like mixing increased (i.e., with reduced contact between vaccinated and unvaccinated subpopulations) … the contribution of risk to vaccinated people caused by infection acquired from contact with unvaccinated people (as measured by Ψ) increased. The larger the value of Ψ, the more unvaccinated people contributed to infections in the vaccinated subpopulation.”

This Ψ (=B_v/f_vu) was introduced ad hoc by Fisman et al., without any reference. To our knowledge, it has no prior use or justification in the epidemiological literature.

Contrary to Fisman et al.’s assertion, Ψ is not a measure of “the contribution of risk to vaccinated people caused by infection acquired from contact with unvaccinated people” (which is B_v) because one divides by all contacts, irrespective of whether the said contacts are benign or infectious, and the ratio of benign/infectious changes significantly with the circumstances. This leads to Ψ exhibiting absurd results, in the circumstances of interest, as shown below.

Furthermore, the Fisman et al. statement that “The larger the value of Ψ, the more unvaccinated people contributed to infections in the vaccinated subpopulation” is mathematically incorrect. The opposite is generally true, as also shown below.

Figs. 1-3, below, show Ψ (left panels) and B_v (right panels) versus η, P_v and VE.

All graphs in Figs. 1-3 use the parameters considered by Fisman et al.: β = 437 (probability of transmission per contact multiplied by number of contacts per year), γ = 73 yr^-1, NI = 0.2, and P_v = 0.8 if not otherwise indicated. Here, NI is the proportion of the unvaccinated population that has pre-existing natural immunity at the outset of the epidemic.

In Figs. 1a and 1b (which have expanded Y-scales compared to Figs. 1c and 1d), we note that B_v decreases monotonically with increasing η, whereas Ψ increases monotonically with increasing η (for VE > NI). According to Fisman et al., this behaviour of Ψ would mean that “the contribution of risk to vaccinated people caused by infection acquired from contact with unvaccinated people” increases with decreasing mixing (i.e., with increasing separation between vaccinated and unvaccinated), and is largest for complete segregation (η = 1), even though B_v itself decreases to zero at η = 1 (for all values of VE, up to 1, see Figs. 1c and 1d and the inset of Fig. 1c), which is impossible.

Fisman et al.’s ill-defined “risk” (Ψ) (“standardized” by an unknown number of infectious contacts) that monotonically goes to its largest value when the agent of risk is removed (η = 1) is an absurdity, of no apparent utility in the real world.

Figure 1: Panels (a) and (c): Fisman et al.’s Ψ index vs the degree of segregation η, for different values of the vaccine efficacy VE. Panels (b) and (d): the fraction of all infections among vaccinated people that derived from contact with unvaccinated people, B_v, vs η, for different values of VE. Panels (a), (b), and (c) have expanded Y-axes, and the inset of panel (c) shows the full span of the Y-axis for the Ψ vs η curves.

This meaningless result of largest “risk” (Ψ) when nothing happens, and increasingly so for increasing VE (when the vaccinated should be increasingly protected), is maintained and amplified for larger values of VE, as shown in Fig. 1c. Here, Fig. 1 illustrates the behaviours as η → 1 (using η = 0.999, 0.9999, …).

Furthermore, the curves with VE > NI (VE = 0.4 through 0.99) in Fig. 1 prove that the Fisman et al. statement “The larger the value of Ψ, the more unvaccinated people contributed to infections in the vaccinated subpopulation” is unambiguously false. We see that the opposite is true: on increasing segregation η, where Ψ increases (left panels), B_v decreases (right panels). B_v is defined “as the share of infections among vaccinated people that were due to contacts with infectious unvaccinated people”, which is exactly the proportion that “unvaccinated people contributed to infections in the vaccinated subpopulation”.

Here (Fig. 1), as the vaccine is made perfectly effective (near-1 values of VE), “the contribution of risk to vaccinated people caused by infection acquired from contact with unvaccinated people”, supposedly and incorrectly represented by Ψ, now diverges (Ψ diverges) to large values, orders of magnitude outside of any reasonable range compared to its values at the lower values of η (Fig. 1c).

On the contrary, for VE near 1, the actual risk B_v does not diverge as one approaches η = 1, and there is virtually no change in B_v versus segregation η, up to nearly complete segregation (Figs. 1b and 1d). It is difficult to reconcile the “disproportionate” risk from the unvaccinated (inferred from Ψ as interpreted by Fisman et al.: “their choices affect risk of viral infection among those who are vaccinated in a manner that is disproportionate to the portion of unvaccinated people in the population”) with B_v decreasing with increasing η (Fig. 1), while being virtually independent of η for large VE (Fig. 1). In plain terms: In the real world, separation from the cause of risk reduces the risk. In the real world, there is no risk to the vaccinated, “disproportionate” or other, from the unvaccinated when VE = 1.

Fig. 1 thus proves that the main stated inference of Fisman et al. based on their Ψ is false.

This should be sufficient to convince readers of the misguided approach of thus introducing Ψ, but there is more.

Fig. 2 shows Ψ and B_v versus P_v, for many values of η. Here, B_v monotonically decreases to zero as P_v is increased to 1, as expected, and has smaller and smaller values for larger and larger values of η.

In contrast, the “contribution of risk to vaccinated people caused by infection acquired from contact with unvaccinated people”, supposedly and incorrectly represented by Ψ, monotonically increases as P_v is increased, and is systematically larger for larger values of η. This would mean that the “contribution of risk to vaccinated people caused by infection acquired from contact with unvaccinated people” increases the more people are vaccinated, and the more the vaccinated are separated from the unvaccinated, up to the extreme values of total vaccination uptake (P_v = 1), and up to total segregation (η = 1), and both total vaccination uptake and total segregation (P_v = 1 and η = 1), which is absurd.

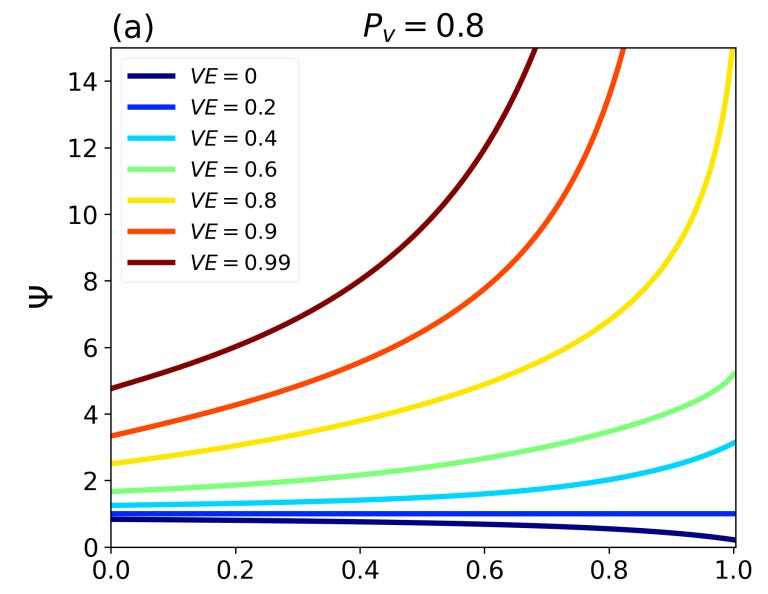
Figure 2: (a) Ψ vs the population fraction of vaccinated people P_v for different values of the degree of segregation η. (b) B_v vs P_v for different values of η.

We learn, for example (Fig. 2a), that the supposed “contribution of risk to vaccinated people caused by infection acquired from contact with unvaccinated people” (Ψ) is approximately “15” at total vaccine uptake (P_v = 1) and for virtually total segregation

(η → 1) when VE = 0.8, which would be a stunning result if it were not meaningless.

In all the Ψ-B_v pairs of curves shown in the two panels of Fig. 2, for each of the values of η shown, the larger the value of Ψ, the smaller the value of B_v (the less unvaccinated people contributed to infections in the vaccinated subpopulation); which again proves that the Fisman et al. statement “The larger the value of Ψ, the more unvaccinated people contributed to infections in the vaccinated subpopulation” is rigorously incorrect.

In every case, we demonstrate that the ad hoc parameter Ψ is not what Fisman et al. believe it to be.

Finally, Fig. 3 shows Ψ and B_v versus vaccine efficacy VE, for many values of segregation η. Here, B_v goes to 1 in the limit as VE approaches 1, trivially because all of the infections of vaccinated individuals must come from unvaccinated individuals as VE approaches 1. Nonetheless, B_v values are systematically smaller for larger and larger segregation η, as expected; and B_v is essentially independent of η when VE is near 1, as also shown above (Fig. 1).

The opposite is true of Ψ (Fig. 3a) and its interpretation made by Fisman et al.: the greater the segregation η, the more Ψ increases; to astronomical values, as one goes to the larger values of VE. This inversion (compared to the behaviour of B_v) would mean that the more one is separated, the greater the danger from being infected by the individuals one is separated from, and all the more so if VE is high. This is difficult to reconcile with reality because it is nonsense, arising from the ill-defined “standardization” used to construct Ψ. 

Figure 3: (a) Ψ vs the vaccine efficacy VE, for different values of the degree of segregation η. (b) B_v vs VE for different values of η.

We hope that this novelty of the Ψ index introduced by Fisman et al. will not spread or persist in the epidemiological literature. It needs to be removed and isolated.

References

Fisman DN, Amoako A, Tuite AR (2022). Impact of population mixing between vaccinated and unvaccinated subpopulations on infectious disease dynamics: implications for SARS-CoV-2 transmission. CMAJ 2022;194:E573-80. https://doi.org/10.1503/cmaj.212105.

Hickey J, Rancourt DG (2022). Viral respiratory epidemic modelling of societal segregation based on vaccination status. medRxiv 2022.08.21.22279035; doi: https://doi.org/10.1101/2022.08.21.22279035.

Citation: Hickey, J. and Rancourt, D.G. “Fisman et al.’s Psi (Ψ) index is ill-defined and leads to absurd interpretations”. CORRELATION Research in the Public Interest, Brief Report, 30 November 2023. https://correlation-canada.org/fisman-et-al-psi-index-is-ill-defined

All CORRELATION reports are here: https://correlation-canada.org/research/

Please support independent research.

And check out my extensive website: https://denisrancourt.ca/